Die unklare Semantik von assoziativen Relationen
Contents
Die unklare Semantik von assoziativen Relationen#
Auch im Umkreis von Semantic Web, Ontologien taucht in breitenwirksamen Illustrationen und Erklärtexten zu “Ontologie” notorisch ein Modellierungselement auf, das in SKOS assoziative Relation genannt wird. Während die Semantik solcher Relationen intuitiv völlig klar erscheint, ist sie bei genauerem Hinschauen weitgehend undefiniert.
Insbesondere sind - so die folgende These - assoziative Relationen weitgehend ungeeignet, um den Begriff und die Leistungsfähigkeit von Ontologien im Sinne Tom Grubers (1995) zu illustrieren.
These:
Tatsächlich sind assoziative Relationen semantisch so unterbestimmt, dass sie sich einer Axiomatisierung geradezu sperren.
Vertikale Relationen#
Vertikale Relationen wollen wir solche Relationen nennen, die “ungefähr” einen Baum aufspannen, und die dafür verantwortlich sind, dass es ein “oben” oder “unten” gibt.
In einer Klassifikation ist es die Teilmengen-Relation
isa, die einen Baum aufspannt;in SKOS ist es die Relationen
skos:broaderTransitive(oder auch nurskos:broader);in einem Thesaurus ist es die Relation broader term (BT);
in einer Meronomy ist es die Relation
partOf.
Diese Relationen wollen wir Baum-Relationen nennen.
ABBILDUNG: intuitive Klassenhierarchie in Protege, mit einer Mehrfach-Vererbung
Baum-Relationen spannen insofern nur “ungefähr” einen Baum auf, weil wir auch Mehrfach-Vererbung zulassen. Je mehr Mehrfach-Vererbungen wir haben, desto mehr verändert sich der Baum zu einem Netzwerk. (Im Unterschied zu mathematischen Sichtweise ist der Unterschied zwischen Baum und Netz also graduell.)
Unabhängig davon, ob wir es mit einem reinen Baum oder einem Netzwerk zu haben, sind diese Eigenschaften bestimmend für solch eine Struktur:
Wir verlangen, dass der Graph gerichtet und azyklisch ist (directed acyclic graph, DAG), und sich also in ein “oben” und “unten” orientieren lässt.
Die Art des Baumes wird über eine einzige “primäre” Baum-Relation definiert. Verschiedene Baum-Relationen werden im gleichen Baum nicht nebeneinander verwendet.
Alle Knoten im Baum sind über die primäre Baum-Relation verbunden.
Im allgemeinen werden Baum-Relationen als transitive Relationen betrachtet; aber Diskussion erforderlich:
Bisweilen wird nur
skos:broadernotiert, wo eigentlichskos:broaderTransitivegemeint ist.Ist
partOftransitiv?
In SKOS werden vertikale Relationen hierarchical genannt.
Assoziative (“horizontale”) Relationen#
Horizontale Relationen wollen wir solche Relationen nennen, die praktisch beliebige Querbeziehungen zwischen einzelnen Knoten in einem Baum (oder Ungefähr-Baum oder einem DAG) aufspannen. Eigenschaften von Bäumen, in die horizontalen Relationen eingezogen sind:
Es gibt keine Einschränkungen bezüglich Zyklen.
Es können beliebig viele unterschiedliche horizontale Relationen verwendet werden.
Nicht alle Knoten sind über dieselbe horizontale Relation verbunden. Im Gegenteil lassen sich Knoten ggf. sogar danach unterscheiden, über welche spezifische horizontale Relationen sie verbunden sind.
Im Allgemeinen wird von horizontalen Relationen nicht angenommen, dass sie transitiv sind.
In SKOS ist die Relation skos:related solch eine horizontale Relation und wird dort semantic relation oder auch associative link genannt (https://www.w3.org/TR/skos-reference/#semantic-relations)
ABBILDUNG: https://www.w3.org/2004/02/skos/core/guide/2005-10-06/img/ex-rel-rel.png Quelle: https://www.w3.org/2004/02/skos/core/guide/2005-10-06/
ex:bird skos:related ex:ornithology .
ex:ornithology skos:related ex:bird .
Zur Vollständigkeit: Von skos:related lassen sich in RDFS dann auch Sub-Properties bilden:
ex:knows rdfs:subPropertyOf skos:related .
ex:loves rdfs:subPropertyOf ex:knows .
SKOS#
Wir haben schon öfters SKOS zitiert, und auch GenDifS exportiert nach SKOS. Wir tun das, obwohl und weil SKOKS ein völlig anderes Konzept der Wissensrepräsentation verfolgt als OWL.
SKOS wurde in der Urform als eine eine (sehr schlanke, schöne) Ontologie in OWL Full (!) publiziert, aber es gibt auch eine praxistaugliche Version in OWL DL. SKOS ist also ein Schema, das sogar als Ontologie formalisiert wurde. Eine in SKOS formulierte Terminologie (mithin also eine Menge von Instanzen) ist dagegen nicht selbst eine Ontologie. Die SKOS-Referenz https://www.w3.org/TR/skos-reference/#L1045 betont diesen Unterschied ganz explizit:
SKOS can, in more advanced applications, also be used side-by-side with OWL to express and exchange knowledge about a domain. […] However, SKOS is not a formal knowledge representation language. To understand this distinction, consider that the “knowledge” made explicit in a formal ontology is expressed as sets of axioms and facts. A thesaurus or classification scheme is of a completely different nature, and does not assert any axioms or facts. Rather, a thesaurus or classification scheme identifies and describes, through natural language and other informal means, a set of distinct ideas or meanings, which are sometimes conveniently referred to as “concepts”. These “concepts” may also be arranged and organized into various structures, most commonly hierarchies and association networks. These structures, however, do not have any formal semantics, and cannot be reliably interpreted as either formal axioms or facts about the world. […]
To make the “knowledge” embedded in a thesaurus or classification scheme explicit in any formal sense requires that the thesaurus or classification scheme be re-engineered as a formal ontology. […] Converting such KOS to a formal logic-based representation may, in practice, involve changes which result in a representation that no longer meets the originally intended purpose.
Taking this approach, the “concepts” of a thesaurus or classification scheme are modeled as individuals in the SKOS data model, and the informal descriptions about and links between those “concepts” as given by the thesaurus or classification scheme are modeled as facts about those individuals, never as class or property axioms. […] these are not facts about the way the world is arranged within a particular subject domain, as might be expressed in a formal ontology.
Semantische Netze#
Assoziative Relationen sind ein wichtiges Element in semantischen Netzen. Die Software CMap beschreibt die Funktion und Bedeutung von sog. “Concept Maps” selbstbezüglich als ein Semantisches Netz:
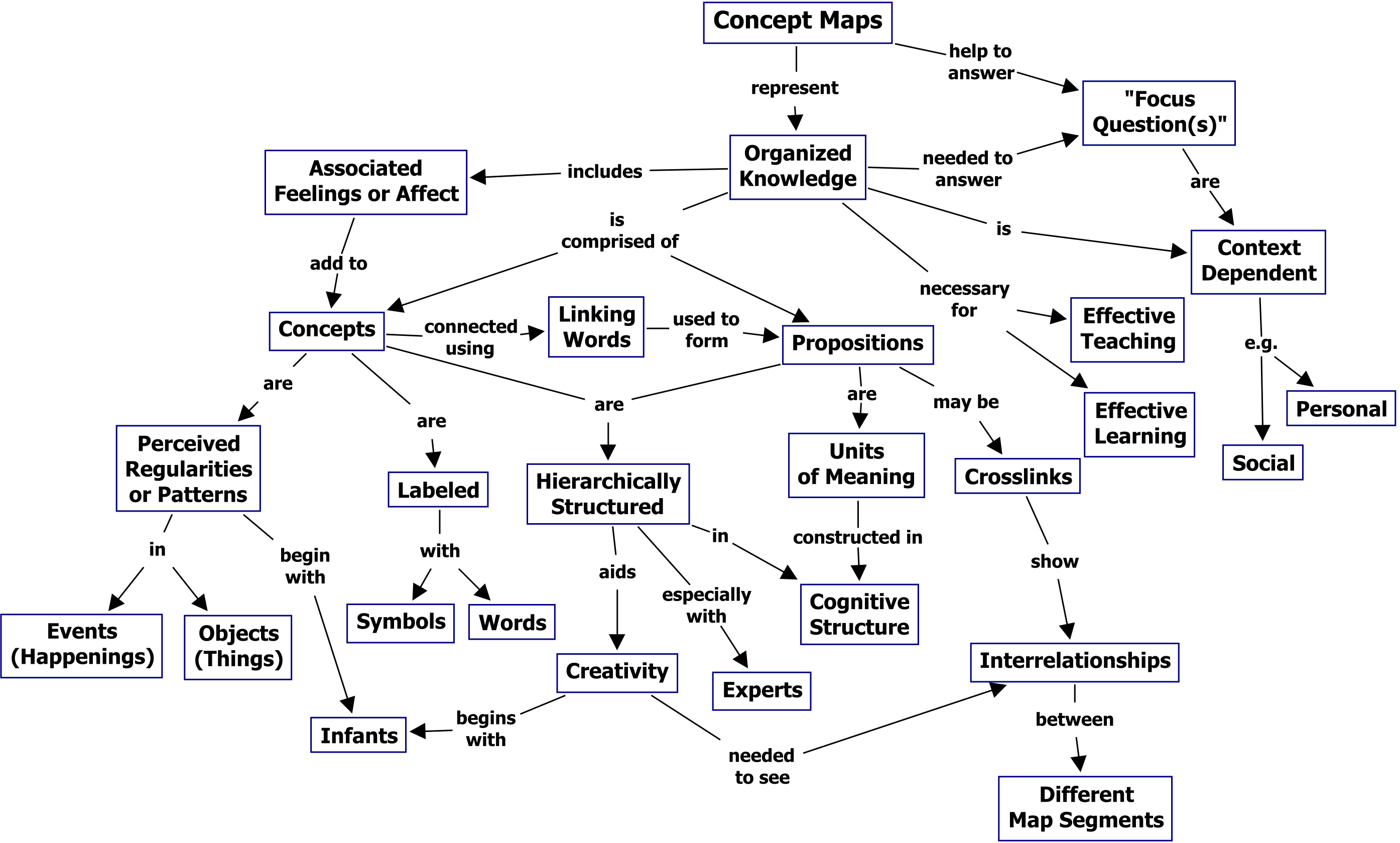
Quelle: https://cmap.ihmc.us/docs/theory-of-concept-maps.php
Dieses Beispiel quillt geradezu über von assoziativen Relationen, bei nahezu völliger Abwesenheit von vertikalen Relationen. In SKOS können wir fast alle dieser assoziativen Relationen als Sub-Properties von skos:related anlegen.
Aber wie sieht das in OWL aus? Gibt es eine “OWL-Semantik” von assoziativen Relationen in einem Semantischen Netz?
Wir nähern uns diesem Problem anhand einer intuitiven Abbildung aus Wikipedia > Semantic network:

(Die aufmerksame Leserin bemerkt, dass in der englischen Version sowohl is an wie auch is a vorkommen. Wir interpretieren diese zwei Relationen hier als Synonyme, mit der Begründung, dass wir solche Netze nicht unmittelbar als ein formales System, sondern zunächst einmal als eine Visualiserung oder Semi-Formalisierung von normalsprachlichen Sätzen verstehen wollen.)
Die Umsetzung nach SKOS ist einfach und straight forward:
Cat,Fur,Mammal,Vertebrawird als Instanz vonskos:Conceptangelegthaswird angelegt als Subproperty vonskos:relatedis_awird interpretiert alsskos:broaderTransitive
Als Ergebnis entsteht - als A-Box der Ontologie SKOS - ein SKOS-Thesaurus. Um so mehr stellt sich die Frage: Welche Semantik könnten wir in OWL vermuten? Dazu müssen wir eine Lösung sowohl für die “vertikalen” Relationen (hier: isa) wie auch die verschiedenen assoziativen Relationen finden.
isa#
Gehen wir in o.A. semantischem Netz von der Ausage Bear has Fur aus. Dann müssen wir entscheiden:
Instanz: Reden wir über einen bestimmten Bär, oder einen prototypischen Bären, den “Bären an sich”?
Klasse: Oder reden wir über die Menge der Bären?
Instanz: isa als element_of#
Wenn man der Instanz-Interpretation folgt, formalisieren wir is_a als is element of. Dann ist Bear ein (bestimmtes oder prototypisches) Element der Menge Mammal, und über diesen Bären sagen wir nun aus, dass er ein (ebenfalls bestimmtes oder prototypisches) Fell hat.
Etwas unklar ist, was in dieser Instanz-Interpretation dann über Mammal ausgesagt wird. Mammal wäre dann ein Element, aber nicht eine Subclass der Menge Animal. Über dieses eine prototypische Exemplar Mammal, sozusagen das Säugetier an sich, könnte man dann problemlos aussagen: Dieses (bestimmte oder prototypische) Tier “Säugetier” hat einen (bestimmten oder prototypischen) Wirbelsäulenknochen.
Diese Instanz-Interpretation erzeugt aber auch ein Problem. Denn leider haben wir auch die Aussage, dass Cat ein Element von Mammal ist. Damit wird Mammal automatisch zu einer Menge, und kann kein (bestimmtes oder prototypisches) Säugetier mehr sein. Solch ein Problem entsteht typischerweise immer dann, wenn man solch eine Interpretation von is a als is element of “schichtet”. In OWL entsteht dann ein sog. OWL-Full-Modell. Dieses wollen wir aber vermeiden, zumindest dann, wenn wir mit formallogischem Inferencing arbeiten wollen, andererseits wir unentscheidbare Logiksysteme erzeugen (Why is OWL Full undecidable?).
Die Instanz-Interpretation scheidet also aus.
Klasse: is_a als is_subclass_of#
Tatsächlich suggeriert die Abbildung, dass wir nicht über einen bestimmten oder prototypischen Bären sprechen, der ein bestimmtes oder prototypisches Fell hat, sonderen allgemein über Bären und Felle und Säugetiere und Wirbeltiere sprechen wollen. Bear und Fur sind also Klassen, und is_a wird als is subclass of interpretiert.
Dann wird aber die Semantik von has unklar. Wenn aber das Subjekt in einer Behauptung Bear has Fur eine Menge ist: Will man dann aussagen, diese Menge habe ein Fell? Das ist natürlich Quatsch. Was man vermutlich aussagen will, ist etwas ganz anderes:
Alle Katzen haben ein Fell!
Unter Berücksichtgung der Unterscheidung von Klasse und Instanz ist vermutlich damit gemeint:
Wenn
cein Element der MengeCatist,dann muss es ein Element
fder MengeFurgeben,so dass wahr ist:
c has f.
Damit ist aber erst die Semantik von c has f thematisiert, mit c und f als Instanzen der Mengen Cat und Fur. Wie formalisiert aber diesen Zusammenhang Cat has Fur korrekt in OWL?
Eine mögliche Lösung ist ausführlich diskutiert und bestens beschrieben an dem strukturäquivalenten Beispiel Healthy_Person has_health_status Good_Health_Value, siehe https://www.w3.org/TR/swbp-specified-values/#pattern2.
Man sieht leicht: Während ein Semantisches Netz straight forward in SKOS modelliert werden kann, ist eine mögliche adäquate OWL-Modellierung recht anspruchsvoll. (Eine andere mögliche Interpretation spezifisch für die Relation has wäre zu finden in Simple part-whole relations in OWL Ontologies. W3C Editor’s Draft 24 Mar 2005). Im Folgenden wollen wir has oder lives in lediglich beliebige assoziative (“horizontale”, nichtvertikale) Relationen betrachten.
rdfs:range oder rdfs:domain?#
RDFS definiert Sprachkostrukte, mit denen man aus existierendem Wissen neues Wissen ableiten kann, sogenannte Entailment-Regeln. Wichtige Entailment-Reglen gibt es insbesondere für rdfs:range und rdfs:domain.
Aus https://www.w3.org/TR/rdf-schema/#ch_domain:
The triple
P rdfs:range Cstates that P is an instance of the classrdf:Property, thatCis an instance of the classrdfs:Classand that the resources denoted by the objects of triples whose predicate isPare instances of the classC.
Aus https://www.w3.org/TR/rdf11-mt/#patterns-of-rdfs-entailment-informative > RDFS entailment patterns (Formatierung und Variablen-Umbenennung JB):
rdfs2:
If S contains
P rdfs:domain X . yyy P zzz .then S RDFS entails recognizing D:
yyy rdf:type X .
rdfs3:
If S contains
P rdfs:range X . yyy P zzz .then S RDFS entails recognizing D:
zzz rdf:type X .
Wichtig zu sehen: Mit rdfs:range und rdfs:domain lässt sich ableiten, dass ein bestimmtes Beispielelement einen bestimmten Typ hat - aber es lässt sich nicht kontrollieren, ob ein bestimmtes Beispielelement einen bestimmten Typ hat. Die Konstrukte rdfs:range und rdfs:domain sind Entailment-, aber keine Constraint-Regeln. Menschen, die den Begriff “Schema” in einem Datenbank- oder XML-Kontext kennengelernt haben, kommt diese Semantik bisweilen unintuitiv vor.
Die obigen Entailment-Regeln haben einen Seiteneffekt, auf den die RDF-Spezifikation explizit hinweist:
Where
Phas more than onerdfs:rangeproperty, then the resources denoted by the objects of triples with predicatePare instances of all [Herv. JB] the classes stated by therdfs:rangeproperties. https://www.w3.org/TR/rdf-schema/#ch_range
Vorsicht Falle: Seien in einem Semantischen Netz die Kanten Bear lives_in Forest und Whale lives_in Water gegeben. Dann wäre es ein schwerer Fehler, diese Semantische-Netzwerk-Tripel in RDFS oder OWL etwa wie folgt zu interpretieren:
:lives_in rdfs:domain :Bear . #1
:lives_in rdfs:range :Forest . #2
:lives_in rdfs:domain :Whale . #3
:lives_in rdfs:range :Water . #4
:theGreatNorthernForest rdf:type :Forest . #5
:Benny_1234 :lives_in :theGreatNorthernForest . #6
Denn dann lässt sich gemäß den RDF Entailment-Regeln für :Benny_1234 aus #6 und #1 ableiten, dass :Benny_1234 ein :Bear ist, sowie gemäß #6 und #3 ableiten, dass :Benny_1234 ein :Whale ist. Und auch Zeile #5 ist redundant, denn diese Typ-Information ergibt sich ja aus #2 - ebenso wie die Information, dass gemäß #4 der :theGreatNorthernForest auch vom Typ :Water ist ;-)
Also: Wenn in einem Semantischen Netz eine Kante wie z.B. “Bären leben_in Wald” ausdrücken soll, dass Tiere, die vom Typ “Bär” sind, immer (notwendig / typischerweise / per default etc.) an einem Ort leben, der vom Typ “Wald” ist: Dann lässt sich das in RDFS oder OWL nicht einfach und geradlinig durch rdfs:range oder rdfs:domain modellieren.
In GenDifS haben wir derzeit keine praxisadäquate Lösung, um REL nach OWL zu übersetzen. Deshalb ist REL bisher ausschließlich aufs SKOS-Ebene implementiert, und zwar straight forward wie oben dargestellt.
frbroo: realises#
Wir haben Relationen mit dem gleichen Namen, aber verschiedenen systematischen bezeichnern, mit unterschidlichem Domain und Range:
R3 is realised in (realises) Domain: F1 Work Range: F22 Self-contained Expression Scope note: This property associates an instance of F22 Self-Contained Expression with an instance of F1 Work. […] This property expresses the association that exists between an expression (F22) and the work that this expression conveys. The semantics of the association will be different depending on what specific subtype of F1 Work the work is an instance of. (frbroo_v_2.4.pdf, p.87)
R9 is realised in (realises) Domain: F14 Individual Work Range: F22 Self-Contained Expression Subproperty of: F1 Work. R3 is realised in (realises): F22 Self-Contained Expression Scope note: This property associates an F14 Individual Work with the unique F22 Self-Contained Expression that completely conveys it.
R12 is realised in (realises) Domain: F20 Performance Work Range: F25 Performance Plan Subproperty of: F1 Work. R3 is realised in (realises): F22 Self-Contained Expression Scope note: This property associates an instance of F20 Performance Work with an instance of F25 Performance Plan that consists of signs (words, figures, etc.) which express the directions the instance of F20 Performance Work consists of.
R13 is realised in (realises) Domain: F21 Recording Work Range: F26 Recording Subproperty of: F1 Work. R3 is realised in (realises): F22 Self-Contained Expression Scope note: This property associates an instance of F21 Recording Work with an instance of F26 Recording realising the instance of F21 Recording Work.
Das kommt öfters vor. Aus Tabelle 2.5.3. FRBR OO Property Hierarchy (p.45 ff):
is realised in (realises): R3, R9, R12, R31, R40
created (was created by): R17, R18; created (was created through): R21,R24; created a realisation of (was realised through): R19, R22, R23
produced (was produced by): R28, R30
assigned (was assigned by): R45, R46, R49, R51, R53; assigned to (was assigned by): R48, R50,
In OO und einer framebasierten Logik - insbesondere F-Logic oder Object Logic - ist das eine ganz normale Modellierung. In einer Description Locic wäre Domain und Range hier eine fehlerhafte Modellierung. Denn die Begriffe “Domain” und “Range” haben in der Objektorientierung eine Semantik, die von “Domain” und “Range” in RDFS und OWL stark abweicht.
In einer Frame-Repräsentation gibt es Frames, die Slots haben. So kann z.B. der Frame “Vortrag” einen Slot “Länge” haben, und auch der Frame “Segelboot” kann einen Slot Länge haben. Um die Aussage “Länge: 27” zu interpretieren müssen wir wissen, welche Länge gemeint ist. Bei mehrdeutigen Slot-Namen lässt sich nicht ableiten, welcher Frame (hier: Vortrag? Segelboot?) gemeint ist, sondern muss man wissen, in welchem Frame er definiert ist. Der Begriff Domäne lässt sich in framebasierten Wissensrepräsentationen verstehen als der Frame, der den jeweiligen Slot definiert.
In RDFS sind Relationen first class objects, die insbesondere auch ohne eine zugehörige Klasse bestehen. Es ist zwar möglich, dass unterschidliche Namen die selbe Relation bezeichnen; aber es ist nicht möglich, dass der gleiche Name unterschiedliche Relationen bezeichnet. Mit dem RDFS-Axiom rdfs:domain (resp. rdfs:range) kann man angeben, welcher Typ sich für eine Instanz ableiten lässt, die als Subjekt (resp. Objekt) in einer Relation auftaucht.